Мир грибов таинственный и до сих пор до конца не изученный.
Когда в Карпатах собирать грибы? Самый простой ответ – с июня по октябрь!
А если вопрос задать по-другому, когда в Карпатах оптимальным образом собирать грибы? Этот вопрос заслуживает особого внимания, и чтобы ответить на него, необходимо обработать статистическими методами многочисленные экспериментальные данные, составить математическую модель и проанализировать ее на экстремумы.
Для каждого ландшафта и каждой территории существует своя цикличность роста грибов, и она действительно имеет место быть! В этом плане очень интересные результаты по белым грибам в Карпатах представил Тимофей Бобичев на основе своих длительных наблюдений.
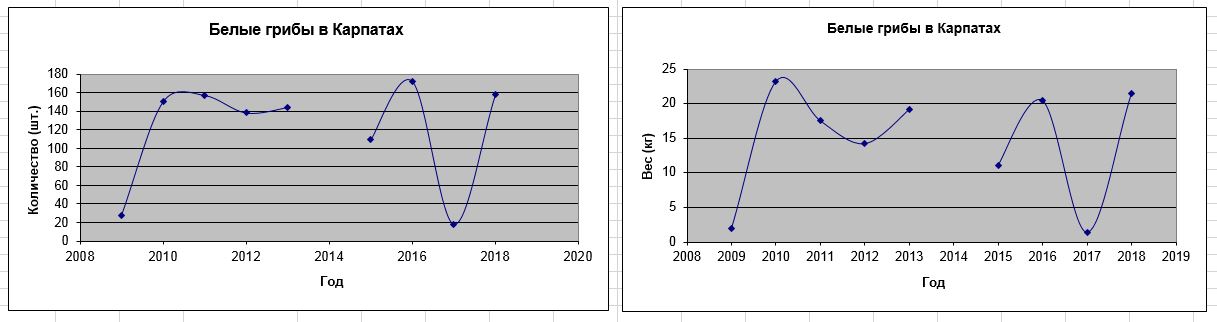
Рис.1. Цикличность грибных периодов. Данные 2014 года отсутствуют, но с большой долей вероятности можно предположить минимум функции в этом году.
Ценность этого графика заключается в том, что экспериментальные данные по белым грибам, а именно они нас в дальнейшем будут интересовать, собраны из одного и того же региона, из одних и тех же грибных мест, и в одно и то же время (конец августа). На обоих графиках видны явные всплески и резкие спады.
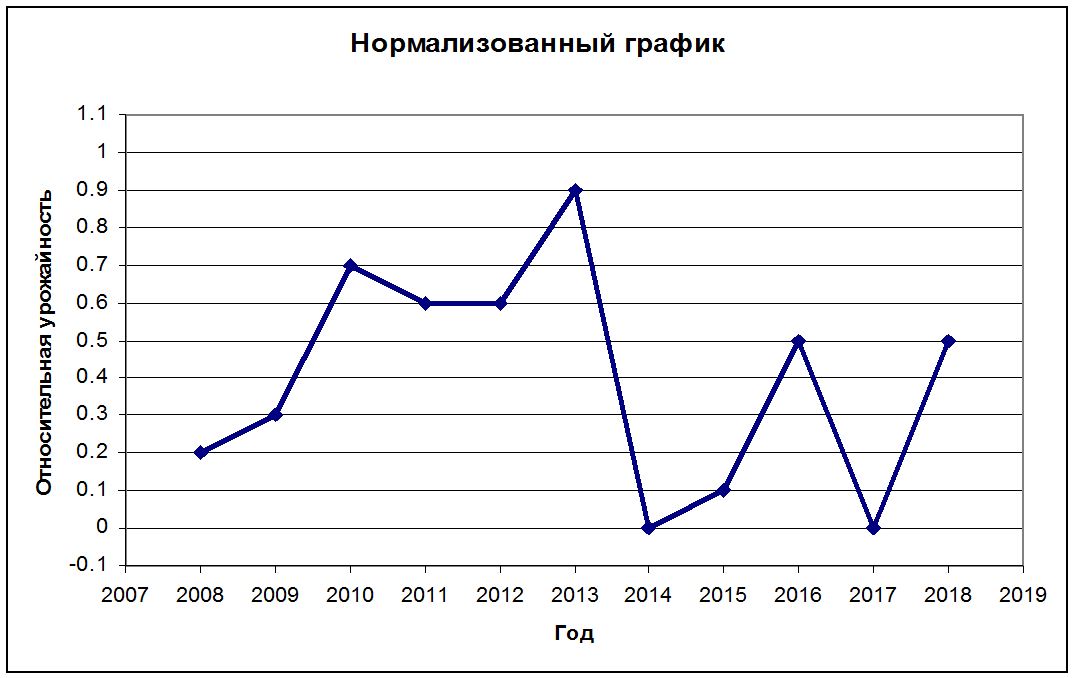
Фактически, нормализованный график с некоторыми дополнениями и уточнениями будет выглядеть так:
Рис. 2. На этом графике четко прослеживается цикличность с периодом три года: 2010, 2013, 2016. Следующий максимум ожидается в 2019 году!
Математическая статистика дает более правильные результаты в том случае, когда рассматривается ансамбль из большого числа частиц. В нашем случае надо было бы учитывать результаты всех грибников, но при этом возникают определенные математические трудности. Всех участников группы надо брать со своим индивидуальным статистическим весом, и в первом приближении условно разделить их на три категории: грибники (стат. вес 1), полу-грибники (1/2) и не грибники (0) (это новички или просто отдыхающие), которые вносят принципиально разный вклад в сбор грибов. Кроме того, не все ведут точный учет, но качественно, результаты у всех совпадают. Поэтому количественные данные Тимофея Бобичева в первом приближении вполне подходят для создания математической модели.
Следующий и самый важный шаг – это подобрать правильно модель, которая соответствовала бы экспериментальным данным. Обратимся к теории биоритмов.
Биологические ритмы (биоритмы), периодически повторяющиеся изменения характера и интенсивности биологических процессов, свойственных живым организмам. Иначе говоря, это «повторение подобного в подобных промежутках времени». Биологические ритмы свойственны растениям, животным, человеку.
Первоначальные хронобиологические (более удачным мне представляется термин «биоритмология») опыты сводились к наблюдению за движением листьев растений в экспериментальных условиях. Затем похожие опыты стали проводить не только на растениях, но и на животных. В дальнейшем эти исследования выявили экспериментальным путем биологические часы у человека. А к какой группе отнести грибы?
Грибы – самая загадочная группа современных организмов, и их классификация связана с наибольшими трудностями.
Когда Линней создавал свою систему, принципы которой до сих пор общеприняты, он не знал куда поместить грибы. Он свалил все, что непонятно, в одну кучу, в том числе и грибы, и назвал это «хаос».
Многие люди считали и продолжают считать, что грибы — это особый вид растений, но на самом деле грибы растениями не являются. До середины 20 века ученые, действительно, относили их к растениям, но потом были сделаны исследования, которые показали, что относить эти организмы к растениям совершенно неправомерно.
Близость грибов к животным подтверждается данными биохимии: у них обнаруживается сходство по многим путям азотного обмена, первичной структуре цитохромов и транспортных рибонуклеиновых кислот. Однако, полностью относить их к классу животных также нельзя.
На данный момент систематики выделяют грибы в отдельное самостоятельное царство живой природы наравне с растениями, животными и бактериями. Тем интересней попробовать применить к ним теорию биоритмов.
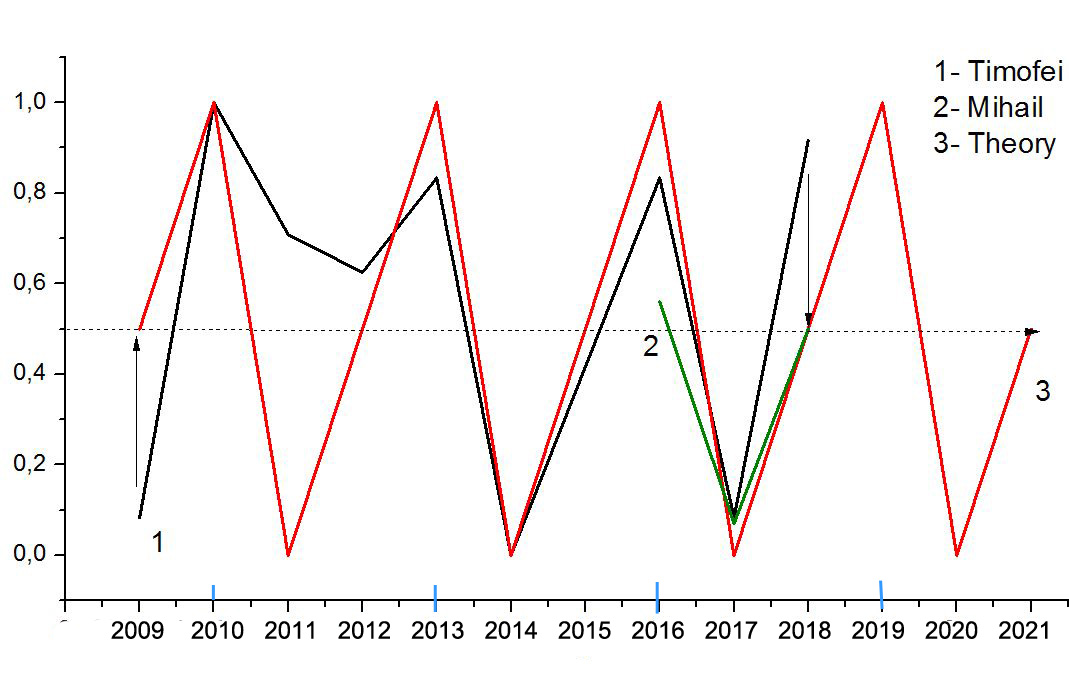
По нашему мнению грибница (мицелии) вполне подпадает под эту теорию, так как она ритмично пульсирует, и самое важное для нас сейчас – это установить период циклов. Я проверил модель с 5-летним циклом, о котором слышал и читал раньше: 2 грибных года, один промежуточный и 2 не грибных. Потом проверил еще 2 модели: симметричную с 4-х летним циклом – грибной, промежуточный, не грибной, и еще раз промежуточный. И, наконец, я рассмотрел 3-х летний цикл: грибной, промежуточный, не грибной. Эта модель лучше всего (можно сказать, идеально!) совпадает с приведенными данными.
Я дополнил эти данные своими наблюдениями за последние три года (я измерял объем засушенных привезенных белых грибов: 2016-9 литров, три 3-х литровых банки; 2017-1 литр; 2018-8 литров) и вот, что получилось:
Рис. 3 Биоритмология белых грибов в Карпатах
Некоторые отклонения в интенсивности на графике 1 (для периода они совершенно не принципиальны) очень легко объяснить. 2009 год был промежуточный, но Тимофей не знал грибных мест, поэтому собрал меньше нормы. 2018 был тоже промежуточный год, но Тимофей знал слишком много грибных мест, поэтому он собрал больше нормы, а в остальные годы все очень хорошо совпало. В 2011 (не грибной по теории год), и он должен был бы найти меньше грибов, но он упорно искал и нашел новые грибные места, поэтому у него положительное дебетовое сальдо. В 2014, где нет данных, я предположил, что у теоретической функции должен был бы быть минимум. Тогда все получается очень красиво! Можно считать, что цикличность у грибов в конкретном регионе Карпат с периодом в три года установлена и доказана.
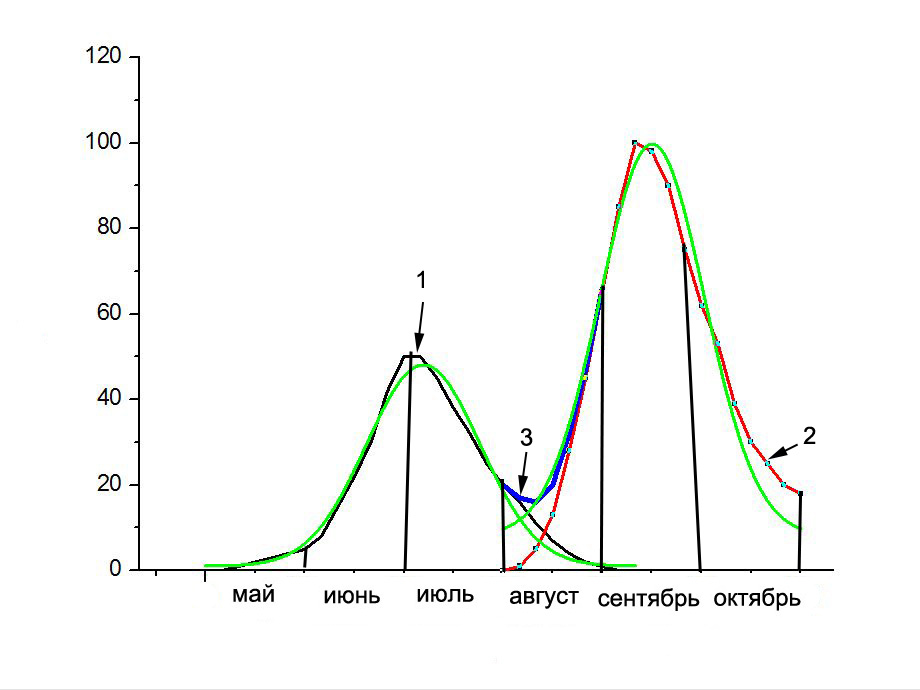
Теперь рассмотрим для каждого года месячную активность роста грибов. Известно, что у грибов есть два цикла или две волны – летняя волна (на рис.4 кривая 1, обозначенная черным цветом) и осенняя (кривая 2-красный цвет).
Рис. 4. Месячная активность роста грибов (1 и 2) и распределение Гаусса-Лапласа вероятности их нахождения (зеленые линии).
Математически эти две волны (1 и 2) прекрасно описываются двумя гауссианами (зеленые графики). Функция Гаусса представляет из себя нормальное распределение, также называемое распределением Гаусса или Гаусса — Лапласа — распределение вероятностей, которое в одномерном случае задаётся функцией плотности вероятности, совпадающей с функцией Гаусса:
где параметр μ — математическое ожидание (среднее значение случайной величины), а параметр σ — среднеквадратическое отклонение (σ ² — дисперсия) распределения.
Как мы видим из графиков вероятности нахождения белых грибов (рис.4), у летней и осенней грибной волны разное математическое ожидание и, как следствие, разная интенсивность. Максимальная интенсивность соответствует осенней волне, которая начинается в августе и продолжается до ноября. Максимум приходится на середину сентября. В августе, когда мы обычно ездим (синим цветом обозначена кривая 3), мы имеем суперпозицию двух гауссианов, т.е. мы находим еще остатки летней волны и уже находим начало осенней волны, но даже при этом общее количество грибов, которое соответствует площади подынтегральной фигуры, значительно уступает сентябрьскому сбору.
В качестве доказательства и подтверждения этой математической теории я приведу несколько фотографий, любезно предоставленных Аней Яремчук, дочкой бабы Дуси, которую вы видите вместе с нами на прошлогодней фотографии.
Посмотрите сколько грибов после нашего отъезда собрала 15 сентября 2018 года баба Дуся вместе с внучкой вокруг своего домика, который расположен рядом с нашей базой.
А так красиво и впечатляюще выглядит в это время дорога на Быстрицу!
Подкованные научными знаниями, мы теперь точно можем рассчитать в каком году и в какое время надо приезжать в Карпаты за белыми грибами.
Выводы: с определенной и достаточно большой вероятностью можно утверждать, что:
1) в Быстрице действует 3-х летний грибной цикл,
2) следующий 2019 год будет очень грибным,
3) лучшее время – первые две недели сентября,
4) в 2020 году можно отдыхать от грибов и ехать в это время купаться в море 
Автор Михаил Назаров
Навигация
Предыдущая статья: ← Карпаты 2018. Часть 5
Следующая статья: Кишинев. Праздник вина 2018 →

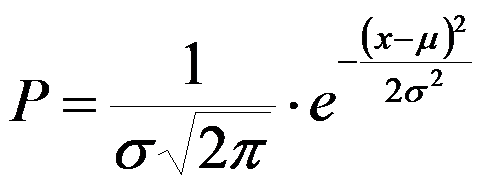



Материал статьи обладает научной новизной и актуальностью. Но есть ряд замечаний:
1. Неплохо бы провести интерполяцию разрывной функции F(t) на рис.1.
2. В статье как-то не хватает использование методов сплайн-аппроксимации (а они явно так и просятся в статью).
3. Ну и конечно наше фсё! – это гармонический анализ. Ну хотя бы банальное преобразование Фурье. Это, как любому известно, позволит выделить основную спектральную компоненту! А она там явно просматривается!
4. Так и осталось неясным из текста статьи – насколько широко пользуется баба Дуся этими полезными результатами? А вдруг она просто так бродит с корзинкой по лесу? – нехорошо это!
Всё-таки я бы направил статью на доработку. Сыровата!